参拾萬仮想大学

【３】４次元立方体の対角線

最終更新：2007年12月18日 22:08

300000

- view

管理者のみ編集可

さて，【まえがき】にも書きましたが，一辺の長さが1cmの正方形（２次元図形）の対角線の長さは $\sqrt{2}$ cm，一辺の長さが1cmの立方体（３次元図形）の対角線の長さは $\sqrt{3}$ cmとなりますので，「じゃあ一辺の長さが1cmの超立方体（４次元図形）の対角線の長さは $\sqrt{4}=2$ cmとなるのかな？」と推測できます。

これについては，【２】４次元の立方体とは違うモデルを用いて考察することにします。

【２】４次元の立方体で，「超立方体は３次元の立方体を第４の方向に平行移動させた軌跡だ」という説明をしました。しかし我々は「第４の方向」がわからないため，しかたなく３次元空間内に「第４の方向」を描いてモデルを作りました。

今度は発想を大胆に転換し，平面（すなわち２次元空間）を勝手に「３次元空間」と思い込むことにしましょう。こう考えることによって，第４の方向を３次元空間の外にイメージしやすくなります。

……と言ったって，言葉の説明だけではわかりにくて当然ですね。次の図を見てください。

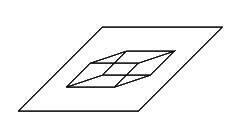
この図は，一辺の長さが1cmの立方体の絵を「平面」に描いたものです。この平面は本当は「２次元空間」ですが，そこに「３次元の立体」を描いてあるということは，言い換えればこの平面の中に「３つの方向を押し込んだ」と考えることができるわけです。

というわけで，以下，この平面を「３次元空間」と思い込んで話を進めることにします。こう考えれば，この「３次元空間」に垂直な「第４の方向」は簡単にイメージできます（下図）

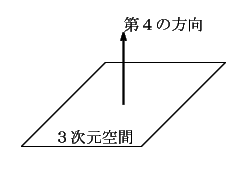
繰り返しになりますが，超立方体は「３次元の立方体を第４の方向に平行移動させた軌跡」でした。そこで，この「３次元空間」に描かれた立方体を，実際に第４の方向に1cmだけ平行移動してみましょう。

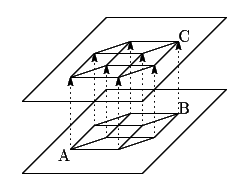
さて，この図の中に「立方体」が何個隠れているでしょうか？　まず上下の平面にそれぞれ１個ずつ，計２個の立方体はすぐにわかりますね。また，それらの立方体の各面は当然「正方形」で，その６枚の正方形を垂直な方向に1cm平行移動したのですから，この平行移動によって６個の立方体が作り出されています。（一辺の長さが1cmの正方形を底面とする高さ1cmの四角柱は「立方体」ですよね!?）

つまり，この図の中に合計で８個の立方体があることがわかりました。この結果は【２】４次元の立方体の説明と一致しています。

ではいよいよ，超立方体の対角線の長さを計算してみましょう。もう一度同じ図を載せておきますので，この図を見ながら読み進めてください。